Table of Contents
What is a Prism?
The Prism is a type of irregular polyhedra, i.e., geometric shapes with all its flat faces.
- But what differentiates a prism from, for example, a pyramid?
- We will learn the characteristics of prisms, the elements that form them, the types of prisms that exist, and what criteria they are classifying.
- We will see how the area and volume of a prism calculate.
- Remember that Polyhedra are geometric bodies whose faces are flat. All facets of a polyhedron are polygons.
- When their faces are all the same, it is a regular polyhedron; if, on the other hand, their faces are different.
- We face it with an irregular polyhedron, as in the case of the prism.
Elements of Prism
The parts of a prism are:
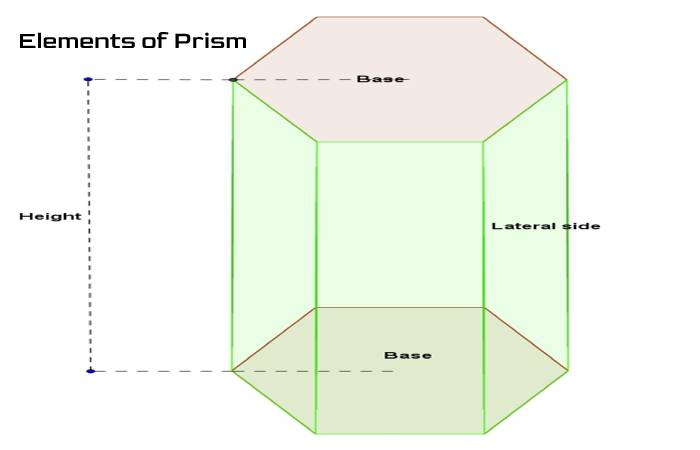
- Bases (B): each prism has two bases, equal and parallel.
- Side faces (C): the parallelograms between the two floors.
- Edge (A): the line segment where two faces meet (both side faces and feet).
- Vertex (V): the point where three or more edges intersect.
- Height (h): the distance between the two bases.
Types of Prisms
We can classify the prisms according to four different criteria:
- Regular or irregular: a prism is standard if its bases are regular polygons and irregular if they are irregular polygons.
- Straight or oblique: The prism is linear when its axis is perpendicular to the bases and oblique when the angle between the axis and the base is different from 90 °.
- Convex or concave: it is convex if its bases are convex polygons and concave if, on the contrary, they are concave polygons.
How to calculate the area of a Prism
- To calculate its area, you have to add the size of each of its faces.
- If it is a straight, it can calculate the area with the following formula:
- Area = 2 × A b + P b × h
Where:
- A b is the area of the base
- P b is the perimeter of the base
- h is the height of the prism
How to calculate the volume of a prism
- The volume of a prism is the product of base area (A b) and the height (h):
- Volume = A b × h
Reflecting prisms

- In reflector prisms where scattering is not desirable, the light beam introduces.
- So that at least one total internal reflection occurs to change the direction of propagation, the orientation of the image, or both.
- In the previous equations, when we have calculated the minimum dispersion.
- We realize that it is independent of the refractive index and the wavelength.
- The reflection will occur without any color preference, and the prism is called achromatic.
- The following figures show some of the many reflector prisms out there, which construct BSC-2 p C-1 glass.
Amici’s Prism
- It is a truncated orthogonal prime with an added roof section on the hypotenuse side.
- It’s most common use has the effect of splitting the image in half and swapping the portions right to left.
- These prisms are expensive because they must keep the apical angle within approximately 3 to 4 arc seconds.
- Otherwise, you will get a bothersome double image.
- It is often used in a simple telescope system to correct for lens reversal.
Penta Prism
- However, it will deflect the beam by 90º without affecting the orientation of the image.
- Note that two of its surfaces must be silver.
- We can you these prisms as reflectors at the ends of short-range finders.


